From the helix of a strand of DNA to the arrangements of protein's building blocks, the twists and swirls of biochemistry often follow a surprisingly consistent orientation of left- and right-handedness known as chirality.
A recent study involving the tesselations of a simple shape based on triangles might help us better understand why biology holds preferences for one orientation over the other.
Conducted by a small team of researchers from the US and Germany, the investigation shows how a combination of geometry and basic physics might be behind some of life's most intriguing patterns.
"The Universe shouldn't favor one handedness over another, but at scale after scale, chiral preferences emerge," Chan Zuckerberg Biohub biophysicist Greg Huber says. "Chirality can be very mysterious."
Much like our two hands held palms up, the mirrored version of chiral molecules can't be aligned perfectly over each other no matter how they're rotated. So while left- and right-handed molecules look nearly identical, they can have radically different impacts on the real world. Using the flipped version of a molecule in a drug, for example, could do harm more than it helps.
It's not just organic molecules that can have an orientation, either. Minerals can be chiral when structured in biological systems. A snail's spiral-shaped calcium carbonate shell and the minerals in our bones are just two examples.
But how these minerals form atom by atom into crystalline chiral shapes is simply another curiosity of chirality.
To better understand the emergence of chirality, especially in the crowded space of a biological system, Huber and colleagues turned to the most basic 2D chiral shape derived from a series of triangles: an asymmetric shape nicknamed the sphinx.
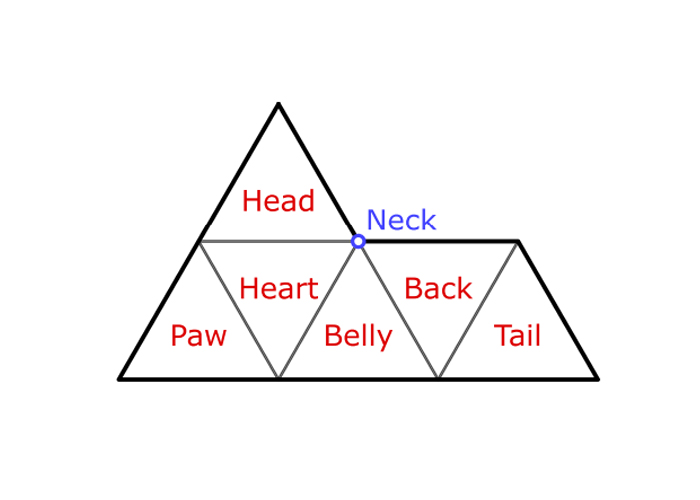
Huber and team used computer models to test the left-and right-handedness of sphinx tile alignments, tesselating them in different numbers and orientations. As the researchers explain in their paper, they wanted "to explore the statistical mechanics of, and to expose the chiral nature inherent in, ensembles of densely packed chiral tiles subject to finite spatial boundaries."
Being asymmetric, sphinx tiles can fit together in many different ways, compared with something as simple as a square. Just two sphinx tiles, for example, can be combined in more than 45 different ways to make a pair, whereas two squares can only go together one way.
As the number of sphinxes in a pattern increases, they combine in super-exponential ways, giving the researchers access to a large, theoretically random system to work with.
Huber and colleagues modeled the interactions between chiral sphinxes under high and low energy conditions, akin to temperature. In high-temperature systems, chiral sphinxes hardly had a chance to interact as they jostled into place and ended up making a jumbled pattern.
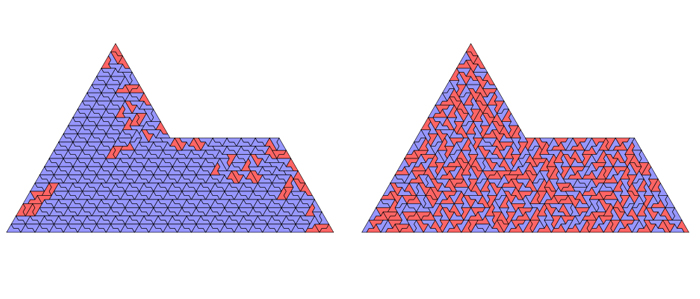
As temperatures lowered, the interactions became more orderly and sphinxes of the same chirality flocked together to form clusters you can see in the diagram above.
Surprisingly, however, in high-temperature systems constrained by a symmetrical outer boundary – like being in a crowded room – sphinxes of the same chirality tended to cluster together as well, as shown in the diagram below.
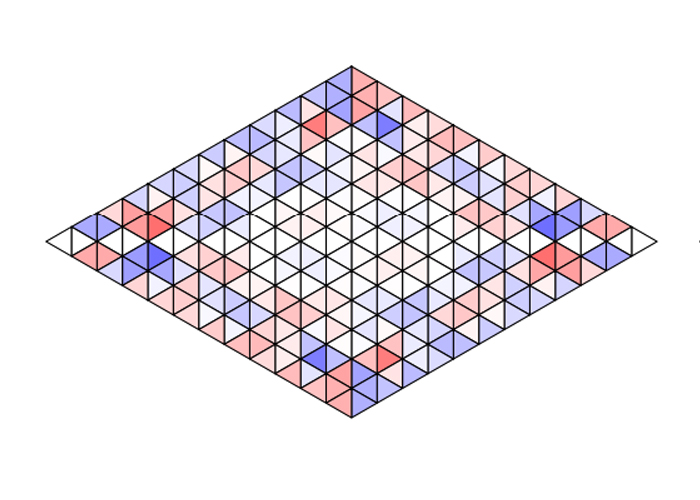
Even in such a basic, stripped-down model of chirality, the modeling shows patterns can arise out of the chaos, and that like molecules seem to gravitate towards like.
Discovering any rules behind these geometric patterns could help researchers across many fields of science, possibly understand the structure of viruses' outer coats or how magnetism might have set off a chain reaction that ultimately gave life its molecular asymmetry.
This research was published in Physical Review Research.
