A pair of Danish computer scientists have solved a longstanding mathematics puzzle that lay dormant for decades, after researchers failed to make substantial progress on it since the 1990s.
The abstract problem in question is part of what's called graph theory, and specifically concerns the challenge of finding an algorithm to resolve the planarity of a dynamic graph. That might sound a bit daunting, so if your graph theory is a little rusty, there's a much more fun and accessible way of thinking about the same inherent ideas.
Going as far back as 1913 – although the mathematical concepts can probably be traced back much further – a puzzle called the three utilities problem was published.
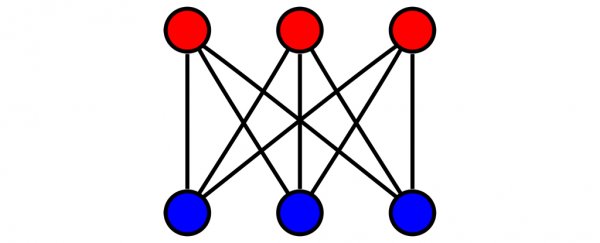
Put simply, imagine there are three houses lined up in a row, which you could draw on a piece of paper. Underneath them, you might also draw three separate utilities: water, gas, and electricity.
Three utilities solution with one line crossing. (CMG Lee/Wikimedia Commons/CC BY-SA 4.0)
The challenge is to draw lines on this simple graph, connecting the three utilities to each house. But there's a problem: none of the lines (nine in total) on the paper are allowed to cross one another. Can you think of a way to join everything up without any of the connections intersecting?
In the most conventional sense – on an ordinary, two-dimensional sheet of paper, as an example of a planar graph – it's not possible to solve the three utilities problem. Inconvenient though it may be, not all of those houses can receive their connections.
But the three utilities problem isn't a puzzle so much to be solved, as rather an example of how some kinds of graph networks are not planar – that is, capable of having edges (lines) connecting their various vertices (houses and utilities) without the lines being crossed.
When you're dealing with more complex graphs that involve more vertices, Kuratowski's theorem helps mathematicians determine whether graphs are planar or not, and since the 1970s, researchers have also been devising algorithms to do the same thing more quickly.
Nonetheless, after one final algorithmic advance in the 1990s, no substantial progress was made in this area for decades, at least not with regard to algorithms that can solve for dynamic (changing) graphs.
Fast-forward to last year, and computer scientists Jacob Holm from the University of Copenhagen and Eva Rotenberg from the Technical University of Denmark were slaving away over the problem.
"We had nearly given up on getting the last piece and solving the riddle," Holm says. "We guessed that there would be another five years of work, at best, before we would be able to solve the puzzle."
It was at that point, almost by accident, they realised they'd effectively already solved most of the problem in another piece of research – a pre-print paper on related planar concepts, which the pair released online in 2019.
With the concealed solution already published, the pair scrambled in the following weeks, writing up a formal proof of their improvement to the graphing algorithm, which hadn't seen enhancement since the 1990s.
"We worked on the article non-stop, for five to six weeks. And, it ended up filling more than 80 pages," Rotenberg says.
The results, now published, provides an algorithm that takes the least computational time yet to solve the question of whether a dynamic graph – subject to insertions and deletions of edges connecting its vertices – can support a planar embedding. (In simple terms, whether it could be drawn on a piece of paper with no lines being crossed.)
It's a big advancement, since the same difficulties present in something as conceptually simple as the three utilities problem become much more unfathomable in fields like microchip design or road planning, where a lot more vertices are involved than simply three houses and three utilities.
"It turns out that for dynamic graph problems it is often possible to build some data structure that can be used to recompute the answer after each change to the graph much faster than recomputing the answer from scratch," Holms explains.
"This result is of course a huge personal victory for us."
The findings are reported in STOC 2020: Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing.