Mathematicians aren't usually the first point of call on moving day. And really, why should they be? For nearly 60 years, they couldn't even tell you whether your fancy new three-seat sofa would make it around the tight corner into your apartment.
Jineon Baek just might change our minds on that. The combinatorics and geometry enthusiast from Yonsei University in Korea has just dropped a 100-page proof on this very problem, solving one of the Universe's most pressing issues so we can all make better furniture choices before we get stuck at the top of the stairwell on the third floor.
In 1966, the Austrian-Canadian mathematician Leo Moser formalized a problem plaguing humanity ever since an exhausted Australopithicus first stood in the far reaches of a cave with a comfy-looking gazelle carcass that just wouldn't budge any further.
On the surface, it seems straightforward. What's the largest two-dimensional object that can successfully make it around an L-shaped corner?
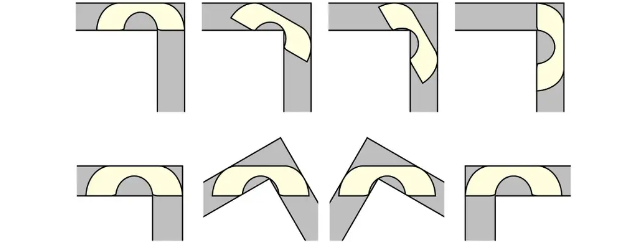
For a corridor one unit across, a chair that's one square unit is a walk in the park. On the other hand, a perfectly rectangular two-square unit will obviously get stuck. Forget anything longer – it now lives in the corridor.
But what if it's some unique IKEA thing named like a Lord of the Rings character and shaped like an old-fashioned telephone receiver?
Just two years after Moser threw down the gauntlet, British mathematician John Hammersley found a sofa consisting of a dissected semicircle separated by a square with a semicircle bite removed (where three friends can awkwardly touch knees as they talk mathematics) could be 2.2074 units in area and still just make it around the corner.
Hammersly also set an upper limit for the design – nothing larger than 2.8284 could squeeze past.
Nearly a quarter of a century passed before a Rutgers University scholar named Joseph Gerver suggested a subtle redesign on Hammersly's sofa, rounding out a few edges with extra arcs and finding a shape that added fractions to the previously lower limit to claim the maximum sofa size is a fraction over 2.2195 units.
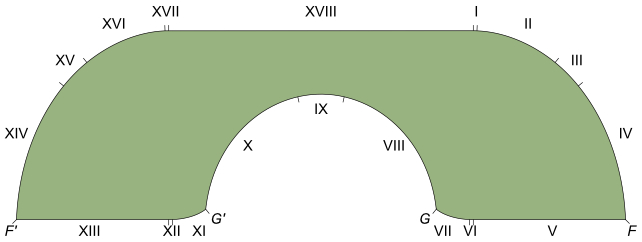
Gerver successfully showed his solution was locally optimal, setting a new lower bound for the maximum area. In other words, his solution was the best within the limited conditions defined by that shape.
Without a universal formula for sofa shapes that describes all possible dimensions of furniture, however, it's difficult to prove a slightly larger sofa with subtly different curves might not make it.
In 2018, Santa Fe Institute mathematician Yoav Kallus and Dan Romik from the University of California, Davis used a computer-assisted scheme to show the sofa could feasibly be as high as 2.37 units.
For this latest proof, Baek applied a bit of mathematical wizardry known as an injective function to map successful shapes of Gerver's sofa, locking down key properties before expanding them through ever larger dimensions to prove once and for all how big a Gerver-like sofa could be.
Sure enough, 2.2195 units is the king of sofas for a 1-unit-wide corridor and an L-shaped corner, just as Gerver had proposed in 1992.
Though yet to be peer-reviewed, Baek's solution could be the final word on the sofa problem, at least in this setting. If you've got a second corner to turn in the opposite direction, we recommend a shape called Romik's ambidextrous sofa.
Now available in aisle 13 at IKEA, next to Gimli's kitchen table.
This research is available on the pre-publish server arXiv.
