Daedalus could have learned a thing or two from a team of physicists in the UK and Switzerland.
Taking principles from fractal geometry and the strategic game of chess, they have created what they say is the most fiendishly difficult maze ever devised.
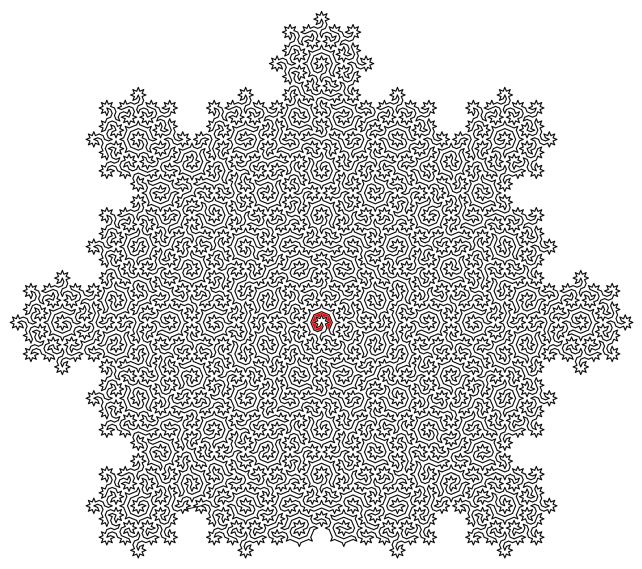
Led by physicist Felix Flicker of the University of Bristol in the UK, the group has generated routes called Hamiltonian cycles in patterns known as Ammann-Beenker tilings, producing complex fractal mazes that, they say, describe an exotic form of matter known as quasicrystals.
And it was all inspired by the movement of a Knight around a chess board.
"When we looked at the shapes of the lines we constructed, we noticed they formed incredibly intricate mazes. The sizes of subsequent mazes grow exponentially – and there are an infinite number of them," Flicker explains.
"In a Knight's tour, the chess piece (which jumps two squares forwards and one to the right) visits every square of the chessboard just once before returning to its starting square. This is an example of a 'Hamiltonian cycle' – a loop through a map visiting all stopping points only once."

Quasicrystals are a form of matter only found very extremely rarely in nature. They're sort of a strange hybrid of ordered and disordered crystals in solids.
In an ordered crystal – salt, or diamonds, or quartz – the atoms are arranged in a very neat pattern that repeats in three dimensions. You can take a section of this lattice and superimpose it on another, and they'll match up perfectly.
A disordered, or amorphous, solid, is one in which the atoms are just all higgledy-piggledy. These include glass and some forms of ice usually not found on Earth.
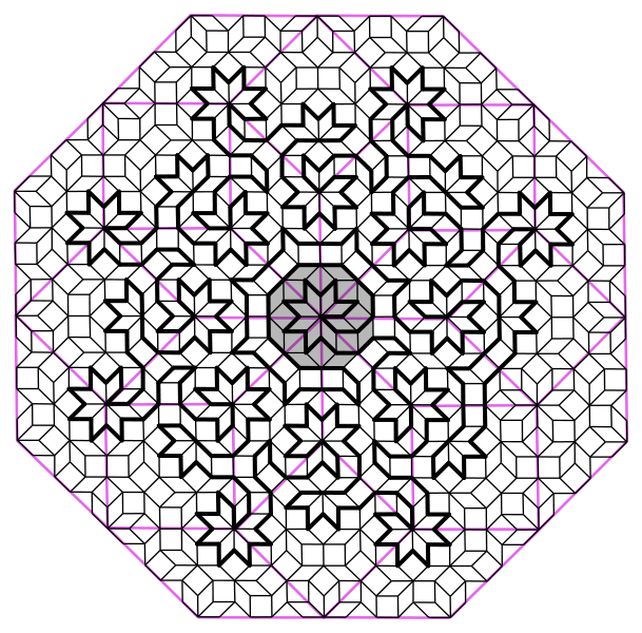
A quasicrystal is a material in which the atoms form a pattern, but the pattern does not repeat perfectly. It might seem pretty self-similar, but superimposed sections of the pattern will not match up.
These similar-looking but non-identical patterns are very similar to a mathematical concept called aperiodic tilings, which involve patterns of shapes that do not identically repeat.
The famous Penrose tiling is one of these. The Ammann-Beenker tiling is another.
Using a set of two-dimensional Ammann-Beenker tilings, Flicker and his colleagues, physicists Shobhna Singh of Cardiff University in the UK and Jerome Lloyd of the University of Geneva in Switzerland, generated Hamiltonian cycles that they say describe the atomic pattern of a quasicrystal.
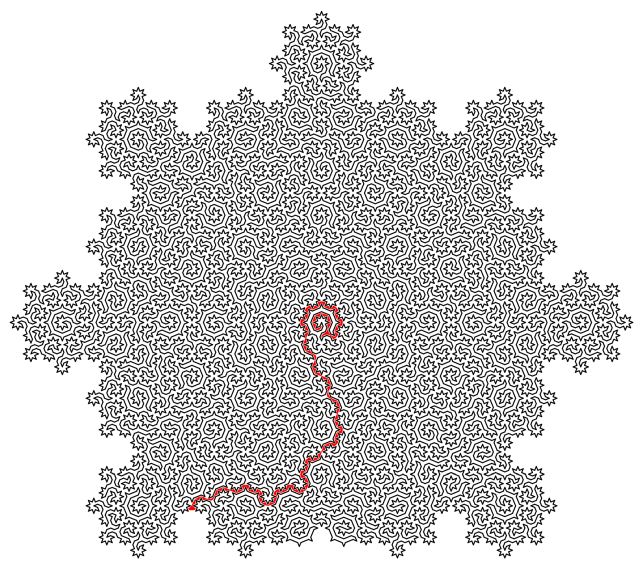
Their generated cycles visit each atom in the quasicrystal only once, connecting all the atoms in a single line that never crosses itself, but cleanly continues from beginning to end. And this can be scaled infinitely, generating a type of mathematical pattern known as a fractal, in which the smallest parts resemble the largest.
This line then naturally produces a maze, with a start point and an exit. But the research has far greater implications beyond entertaining antsy children in diners.
For one, finding Hamiltonian cycles is extremely difficult. A solution that would allow for Hamiltonians to be identified has the potential to solve many other tricky mathematical problems, from complex route finding systems to protein folding.
And, interestingly, there are implications for carbon capture via adsorption, an industrial process that involves hoovering up molecules in a fluid by sticking them to crystals. If we could use quasicrystals for this process instead, flexible molecules could pack themselves more tightly by lying along the Hamiltonian cycle therein.
"Our work also shows quasicrystals may be better than crystals for some adsorption applications," Singh says.
"For example, bendy molecules will find more ways to land on the irregularly arranged atoms of quasicrystals. Quasicrystals are also brittle, meaning they readily break into tiny grains. This maximizes their surface area for adsorption."
And if you happen to have a minotaur you need to stash away somewhere, we think we know someone who can help.
The research has been published in Physical Review X.
